PEST
“PEST” stands for “parameter estimation”. It adjusts a model’s parameters in order that model outputs match field data. The model can be arbitrarily complex. PEST’s interface with the model is non-intrusive.
PEST can work in a highly parameterized world; it can adjust thousands of model parameters. As is explained in the PEST book (and lots of other places) this is important, particularly when calibrating environmental models such as groundwater models. Reasons include the following:
- Information contained in measurements comprising a calibration dataset can flow freely to model parameters in ways that allow these parameters to best represent spatial variability of system hydraulic properties;
- Parameter and predictive bias is minimized;
- Evaluation of post-calibration uncertainty is not compromised by failure to represent potential heterogeneity of system properties. (The parameters that cannot be estimated are just as important as those that can be estimated when calculating the uncertainties of decision-critical predictions.)
Specifications of PEST’s inversion algorithm include the following:
- Linear and nonlinear Tikhonov regularization;
- Inverse problem solution using singular value decomposition and LSQR;
- Efficient SVD-assisted inversion using “super parameters”;
- Jacobian matrix evaluation using low or high order finite differences;
- Efficient parameter bounds enforcement;
- Flexible definition of the objective function minimized through history-matching process;
- Comprehensive reporting of inversion outcomes.
PEST_HP is a version of PEST whose algorithm is optimized for use in parallel computing environments. In addition to those of PEST, its capabilities include the following:
- Optional Jacobian matrix evaluation using random and simultaneous parameter increments (this considerably reduces the number of model-runs required to populate a useable Jacobian matrix);
- Secondary parameters calculated from primary parameters;
- Flexible, adjustable use of Marquardt lambda and Broyden Jacobian updating when testing parameter upgrades;
- High speed matrix manipulation and decomposition using the Intel MKL library;
- Conjunctive use of simple and complex models;
- Dimensional reduction using ensemble space inversion (ENSI).
- Parallelized, repetitive running of a model for any purpose.
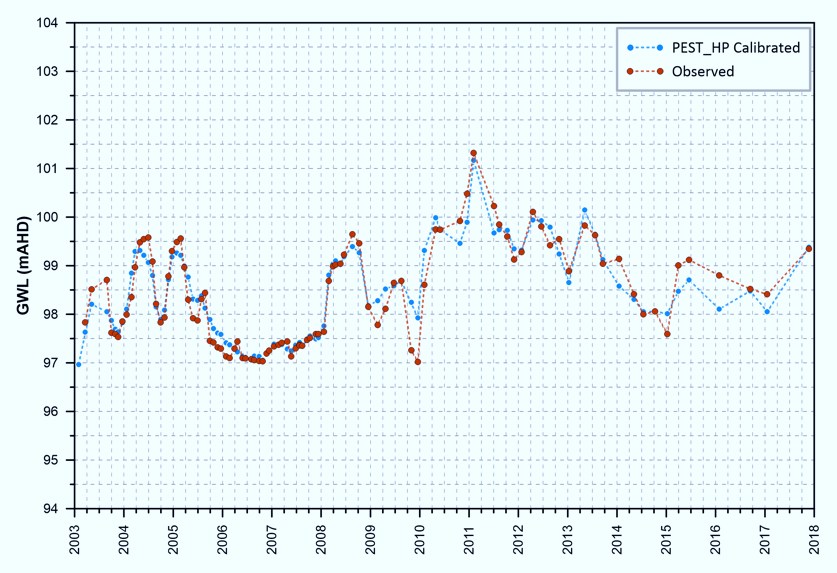
PEST and PEST_HP can be used to calibrate a model of arbitrary complexity. They can also be used to adjust random parameter fields in order to minimize model-to-measurement misfit, thereby implementing the randomized maximum likelihood method of sampling the posterior parameter probability distribution. Using PEST’s linear analysis utilities, pre-adjusted random parameter fields can sample a good approximation to the true posterior parameter probability distribution. Adjustment of these fields can then be undertaken using the same, pre-calculated, Jacobian matrix. When combined, these measures enable efficient sampling of the true posterior parameter probability distribution. These samples then form the basis for exploring parameter and predictive uncertainty.
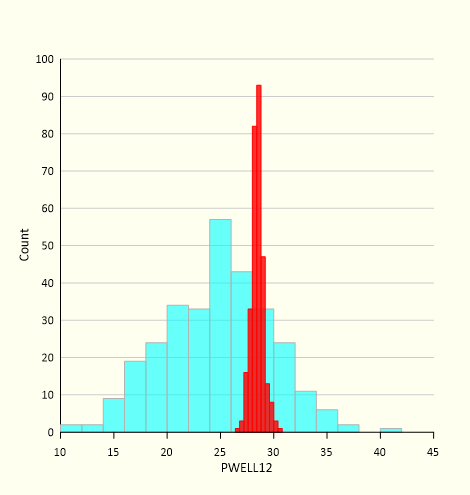
Both PEST and PEST_HP can also be run in “pareto” mode to implement direct predictive hypothesis testing as a flexible methodology for probing posterior predictive uncertainty. This methodology does not suffer from errors incurred by improper definition of the prior parameter probability distribution.
Data Space Inversion
Data space inversion (DSI) offers an extremely efficient way to quantify and reduce the uncertainties of predictions made by models of arbitrary parametric and/or structural complexity. In fact the concept of "parameters" loses its meaning.
A model is run a few hundred times - over the past and into the future. On each occasion that it is run, the model is equipped with a different random realization of hydraulic properties. These hydraulic properties can be expressed in non-adjustable, categorical ways, using complex geostatistical simulators. Model outputs of interest are system states and fluxes that match the contents of a calibration dataset (when it is run over the past), and predictions of management interest (when it is run into the future).
On the basis of these model runs, program DSI2 (supplied with PEST) can then build a statistical model that links the measured past to the managed future. This statistical model can then be conditioned on the actual calibration dataset. The outcomes of the conditioning process are predictions of maximum posterior likelihood, together with their posterior uncertainties.
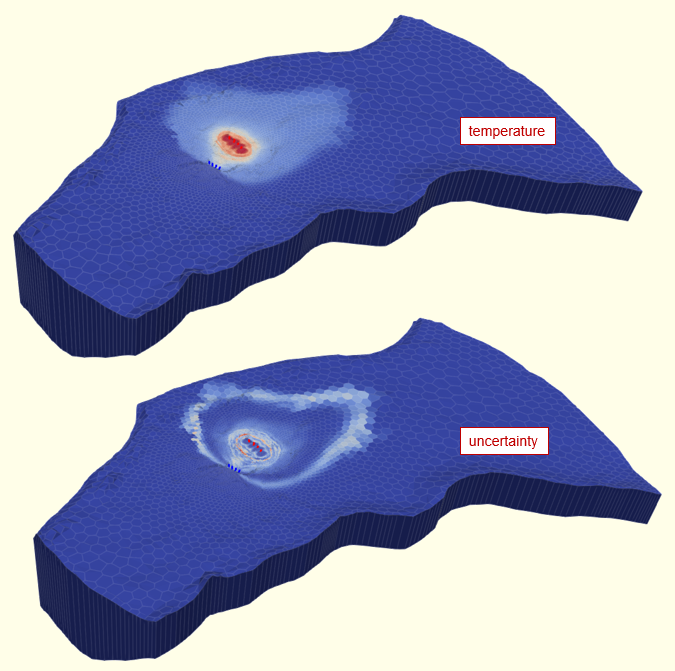
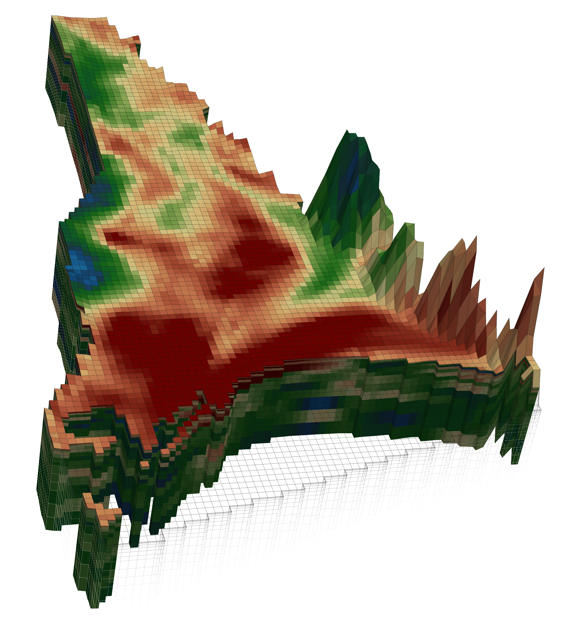
The figure below is taken from a GMDSI slideshow and accompanying tutorial. It shows the predicted disposition of a heat plume following 30 years of operation of a shallow, open-loop geothermal system. The model employs complex hydraulic property fields based on non-stationary geostatistics. The calibration dataset is comprised of heads and river inflow. No adjustment of hydraulic property fields is necessary in order to quantify and reduce the uncertainties of heat plume predictions.
Ensemble Space Inversion
Ensemble space inversion (ENSI) achieves dramatic increases in model run efficiency and history-matching alacrity through dimensional reduction. It works in a subspace that is spanned by random realizations of hydraulic property fields of arbitrary complexity. In this way it is somewhat similar to ensemble methods. However ENSI subspaces are more flexible because they can be defined differently for different hydraulic property types. Individual model parameters can be estimated at the same time.
This flexibility of subspace definition, combined with Broyden Jacobian updating performed by PEST_HP, often allows good model-to-measurement fits to be attained in a remarkably small number of model runs. Estimation of native model parameters simultaneously with factors applied to realizations of hydraulic properties enables good ENSI performance in highly nonlinear contexts. These include hierarchical inversion wherein geosatistical hyperparameters which define the nature of heterogeneity are estimated along with so-called "iid parameters" that define the locations of heterogeneity. ENSI can therefore complement nonstationary stochastic field functionality offered by PLPROC and members of the Groundwater Utility Suite.
Other Model Dancing Partners
Other dancing partners supplied with the PEST suite are now briefly described. These are downloaded automatically if you download PEST and/or if you download PEST_HP. Most of these programs can be used interchangeably with PEST because they read the same control file as that which PEST reads, and because they interact with a model using the same non-intrusive interface that PEST uses.
JACTEST and JACTEST_HP
JACTEST and JACTEST_HP undertake sequential or parallelized model runs based on incrementally-varied parameters. The outcomes of these runs allow a user to evaluate the integrity of sensitivities of model outputs with respect to parameters calculated using finite parameter differences. The existence and extent of numerical granularity associated with model outputs can thereby be assessed.
SCEUA_P
SCEUA_P implements global optimization using the Shuffled Complex Evolution method. Use of this algorithm can sometimes overcome obstacles to a parameter estimation process posed by local objective function optima.
CMAES_P and CMAES_HP
CMAES_P and CMAES_HP implement global optimization using the Covariance Matrix Adaption scheme. Use of this algorithm can sometimes overcome obstacles to a parameter estimation process posed by local objective function optima.
CMAES_P has been used to optimize the design and operation of wellfields to achieve contaminant containment. CMAES_HP includes the option to use so-called “file parameters”. These are random parameter fields; optionally, these random parameter fields can be calibration-constrained. Inclusion of these parameter fields in an optimization process allows a user to accommodate parameter uncertainty when optimizing system management. The risks associated with system management, and the possibility of management failure, can thereby be taken into account.
RSI_HP
“RSI” stands for “realization space inversion”. This achieves history matching using ensembles of parameters. Though its capabilities do not match those of the PESTPP-IES ensemble smoother (it permits no localization), it can often achieve extremely rapid matching of model outcomes to field measurements by simultaneous adjustment of a relatively small number of realizations of an arbitrarily high number of parameters. In doing so, it can yield rapid estimates of posterior parameter uncertainty.
